| Section | Page | Comment | Links |
|---|---|---|---|
| 1.2 | 6 | On the fifteenth line from the bottom of the page there is a missing period: "...elementary events The whole..." should be "...elementary events. The whole..." | |
| On the eighth line from the bottom of the page, the first H1 should be complemented. | |||
| 1.8 | 16 | The program for extracting one element of a vector has [5] when it should have been [3]. | Program |
| The last line on the page should be " [1] 1 0 1 1 1 0 1 0 0 0". | Program | ||
| 1.10 | 26 | The probability in the answer to Exercise 1.16 is correct, but the formula is wrong. Using the answer to Exercise 1.8, the formula should be: P(D1)=1/6+1/6+1/6-2/36-2/36-2/36+3/216 = 25/72 | |
| 2.5 | 35 | On the first line of this section, "are the subsets if" should be "are the subsets of" | |
| 2.7 | 42 | The program
in the answer to Exercise 2.14 assumes sampling with replacement.
If one uses sampling without replacement, the program is:
> 1-choose(380,5)/choose(400,5) [1] 0.2272444The problem, as stated, did not make it clear which was intended. The ambiguity between sampling with and without replacement is a common one, but it only matters when the population is very small. For a small sample from a large population, the effect of the ambiguity is negligible. In this case, the ambiguity has no effect on the conclusion that the smuggler has a roughly 1 in 4 chance of getting caught. | |
| 46 | On line 19, the program for computing the probability of horoscope coincidence has a plus sign that should be a minus sign. One should subtract M*log(N). | Program | |
| 3.1 | 50 | On line 14, "to a generate" should be "to generate." | |
| 52 | Add the following before the program at the bottom of the page: "Of course, one must adjust for the fact that the R geometric distribution is not what we are calling the geometric distribution. To use the R geometric functions for the distribution of W1 one must shift the support by 1." and subtract 1 from the support in all calls to dgeom. | Program | |
| 54 | On line 13, the tabulation of waiting times in the Bernoulli process specifies 10000 points but it should have been 1000. | Program | |
| 55 | The program for computing various negative binomial distributions for a fair coin is the same as the previous program. It should have been this program. | Program | |
| 58 | The programs for animating the binomial distribution for various biases have an extra parenthesis in the last lines. See the links for the correct programs. | Program 1 Program 2 | |
| 3.3 | 61 | In the formula on line 19 (or equivalently, 18 lines from the bottom of the page), the second event should use the random variable Sn, not S'n. | |
| 62 | On the fifth line from the bottom, the probability should be qm-1p. The factor of (n-1) was inadvertently copied from the expression below. Indeed, n has no meaning in that expression. | ||
| 3.7 | 83 | On the third line from the bottom, the reference should be to Section 7.1, not 6.3. | |
| 4.0 | 88 | On the third line from the bottom, the constraint x>0 should be x>a. | |
| 4.1 | 91 | On the fourth and fifth lines from the bottom, X1>y should be X1>t. | |
| 4.2 | 96 | On line 9, the integral should equal 1 not 0. | |
| 4.5 | 101 | The first formula on the page should have n!/an for the joint density of the order statistics. | |
| 4.6 | 103 | On the eleventh line from the bottom of the page, the formula for the density of the beta distribution should raise a to the power k+l-1. | |
| 4.8 | 106 | On the last line, the word "last" should be "least". | |
| 4.9 | 114 | On the second line from the bottom, it should be the (n-1)st order statistic, not the (n-2)nd order statistic. | |
| 115 | On line 15, the interval should be [0,a], not [0,q]. | ||
| 115-116 | In the Answer to 4.16, the gap indices should not be in parentheses. This indicates the order statistics of the gaps, which are not introduced until Exercise 4.20. | ||
| 116 | On the twelfth line from the bottom of the page, the program for computing the distribution of the smallest piece of broken DNA molecule computes the minpiece probability incorrectly: it should be complemented. | Program | |
On the second last line, the program for computing the confidence interval of the smallest piece of a broken DNA molecule uses pts when it should use m. | Program | ||
| 5.2 | 127 | On line 11, there is a missing factor of y in the first integrand. | |
| 5.3 | 130 | The labels on the graphs in the figure are mislabeled. The narrowest (tallest) graph has variance 1/4, while the broadest (shortest) graph has variance 4. | Graph Program |
| 131 | There are two sample variances, one when the mean is known and another when the mean is unknown. When the mean is unknown, the sample variance should have two overbars to indicate the "double" estimation that is taking place. When the mean is known, the sample variance should have a single overbar. So the sample variances shown on page 131 should have double overbars. | ||
| 5.6 | 140 | The definition of tail event should use ≤ rather than = so that it applies both to discrete and to continuous random variables. | |
| 5.8 | 144 | In Exercise 5.9(c), the random variable should be Y. | |
| 148 | In Exercise 5.27, "examination are" should be "examination is." | ||
| 151 | In Exercise 5.47, omit "By means of the runs test." The runs test is not appropriate for this exercise. | ||
| 153 | In Exercise 5.55, one must assume that the random variables are independent. In addition, some of the inequalities were reversed: ε should be greater than 0, and the probability should be greater than 1-ε. | ||
| 5.9 | 154 | On the third line from the bottom of the page, Cov(L1,L2) should be -Var(L1)/n. | |
| 155 | On the seventh line from the bottom of the page, the covariance of the gaps is negative, so the signs should be reversed for the two expressions for Cov(L1,L2). | ||
| On the fifth line from the bottom of the page, the variance of the kth order statistic is the difference of the two quotients, not the sum. | |||
| 159 | The program that computes the normal model of significance for a manufacturing process has sapply(s,n) but it should have sapply(support,n). | Program | |
| 6.1 | 170 | In the second last line of this section, just before the beginning of section 6.2, Yn was typeset as Yn twice. | |
| 6.2 | 170 | The expression on the third line from the bottom is making use of the convention mentioned earlier on the page of leaving a value implicit. It would be better to be more explicit by writing Ti+1=n rather than just Ti+1. | |
| 171 | The overbrace on line 6 was typeset incorrectly: it should not include the final n coin tosses. The formula above the overbrace is correct and makes this clear. | ||
| 6.3 | 173 | Line 12 should be "+ P(A|X1=0,Bh≥t)P(Bh≥t)" | |
| On line 14, the probability is v not u. | |||
| On line 16, the first equation should be v=P(A|X1=0) | |||
| 174 | On the eighth line from the bottom of the page, a parenthesis was misplaced: P(X2)=0 should be P(X2=0). | ||
| 6.4 | 177 | On the eighth line from the bottom of the page, the denominator should be t not x. In other words, the conditional probability is 1-((t-x)/t)k-1. | |
| 178 | The reference to Section 4.1 should be to Section 4.5. | ||
| 179 | On line 12, the probability should be complemented: 1-((a-x)/a)n-1. | ||
| 6.5 | 181 | On line 7, P(Y≤s|B) should have been been differentiated in an expression like this d/dS(P(Y≤s|B)). | |
| 6.6 | 183 | At the end of the last line of the page, Ba,n should be Bt,n-1. | |
| 184 | In the formula that is 6 lines from the bottom, the denominator has an extra exponent of n-1. The denominator should be (a-t1)n-1. | ||
| 6.7 | 187 | The parentheses are missing or misplaced on the ninth line. It should be P(g(X)≤x) = P(G(g(X))≤G(x)) = P(X≤G(x)) = F(G(x)). | |
| 6.8 | 196 | In Exercise 6.39, compute the ratio of the expectations. The distribution of the ratio of the lengths is the subject of Exercise 6.40. | |
| 196 | Exercise 6.40 ends with, "Do the same for a molecule broken into three pieces." This is redundant: it is Exercise 6.41. | ||
| 198 | In Exercise 6.52, to be consistent with the notation in the referenced section of the textbook, the density should be f(x). | ||
| 6.9 | 206 | In the answer to Exercise 6.33, the subscripts of L should not have parentheses, and X(n-2) should be X(n-1). | |
| 7.1 | 212 | In the middle of the page, the formula for the probability of a nearest neighbor start being more than r units away is exp(-4απr3/3) | |
| 7.2 | 216 | The bracketed expression [0, therandomvariablea] in the definition of Un, a(t) should be [0, a] | |
| 217 | On the last line of the page, the exponent should be n-1. | ||
| 7.5 | 232 | In Exercise 7.19 the size of the class should be 20 not 50. | |
| 8.2 | 244 | On line 15 the formula is computing the probability P(Bt) using the Law of Alternatives. It is not computing the event Bt. | |
| 8.3 | 245 | Fourteen lines from the bottom of the page, the formula for the Laplace transform should be E(e-tA). | |
| 246 | The expression P(t>t) should be P(T>t) | ||
| 8.5 | 251 | On the fourth line of this section, the sum should begin with X1 not Xl. | |
| 8.6 | 253 | On the last line of this section, there is a spurious factor of α. The last sentence should begin with "The parameter pi is the probability..." | |
| 8.9 | 262 | On line 14, the conditional probability is approximately 0.06, not 0.02. Consequently, observing symptom F has increased the probability of the disease to about 6 times the a priori probability. | |
| 8.11 | 267 | On line 3, λ should be set equal to α+β. | |
| 9.3 | 291 | Twelve lines from the bottom of the page, the expectation should be E(log(X))=-1/n. | |
| 9.4 | 293 | On the tenth and third lines from the bottom of the page, the power of w should be a power of 2. | |
| 296 | In the middle of the page on line 16, there is a multiple sum over the product of the random variables Yi. This is a sum over the blocks in the joint partition. It would have been better to have a separate description of the summation rather than try to write it using indexes. In any case, the last (innermost) summation should have been over in such that Xn=in. | ||
| 10.2 | 309 | On line 3, X1 should be set equal to j-1, and on line 4, X1 should be set equal to j+1. | |
| Twelve lines from the bottom, aj should be αj. | |||
| 10.5 | 319 | On line 6, pij(n) should be pji(n), and on lines 12 and 21, there is a spurious subscript j on a. | |
| 10.8 | 332 | In Exercise 10.10, "...loan an the..." should be "...loan on the..." | |
| In Exercise 10.12, there are initially only molecules of types A and B. The general case is discussed in Exercise 10.14 later on the same page. | |||
| 333 | On the eighth line from the bottom of the page, the expression for p should be P(Xt+1|Xt=home) | ||
| 10.9 | 339 | In the answer to Exercise 10.12, there are actually n+1 variables where n=N/2. | |
| A | 347 | The subscripts of S' on line 16 should be S2k'=0, S2k+2'≠0, S2k+4'≠0, ..., S2n'≠0, and on line 22 they should be S2'≠0, S4'≠0, ..., S2n-2k'≠0. | |
| 348 | In the equations on lines 7 to 4 from the bottom, there should be powers of 2 not powers of s, and on the last line, P2n-2k should be L2n-2k. | ||
| B | 351 | The equation that is 9 lines from the bottom should be P(W>t+s)=P(W>t)P(W>s). | |
| 353 | On the sixth line, the interval should be [0,1] and on the fifth line from the bottom, the interval should be [0,a]. |
 |
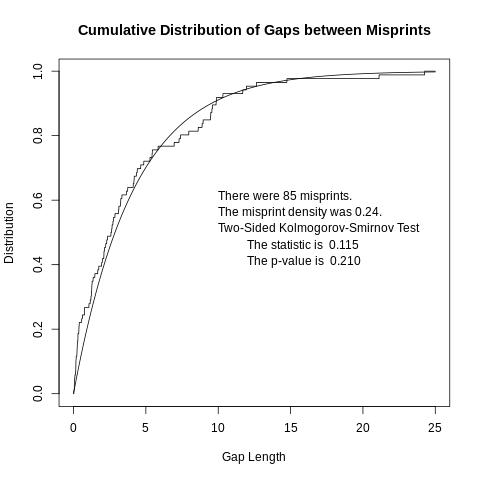
If we model the location of misprints using a Poisson process, then the gaps between misprints should be independent exponential random variables. The position of each misprint includes both the page and the position of the misprint on the page. The gaps were computed, tabulated and plotted. The corresponding exponential distribution was also plotted. The result seems to be reasonably similar to the exponential distribution. To test whether this is a reasonable hypothesis, the two-sided Kolmogorov-Smirnov Test was applied, treating the observed gaps as a random sample. The results were reported in the graph. At the 5% significance level, one cannot reject the hypothesis that the misprints form a Poisson process. |
Special thanks to Tianhua Niu, Thomas Chapuis, Ozan Aksoy, Charles Saunders, Daniel Viar, John Bottoms, Roger Pinkham, Tom Petersen, Anders Sune Pedersen, Peter Paprzycki and Arjun Maneesh Agarwal for contributing to this page.
© 2008, 2009, 2010, 2013, 2020, 2025 Kenneth Baclawski.